A few days ago I wrote about some math behind a scenario where you're trying to identify a new epidemic based on signals proportional to incidence, and ended up deriving:

$$\frac{i\left(t\right)}{c\left(t\right)}=k=\frac{\ln \left(2\right)}{T_d}$$

Where:

• $i\left(t\right)$, is incidence ("how many people are getting sick now")
• $c\left(t\right)$, is cumulative infections ("how many people have gotten sick so far")
• $k$, is the exponential growth rate.
• $T_d$, is the doubling time (redundant with $k$).

One big problem with this model, however, is that any conclusions you make today aren't driven by current incidence, but instead some kind of delayed incidence. There is, unavoidably, time from infection until you're making your decision, during which the disease is spreading further:

If your signal is "people arrive at the hospital and the doctors notice a weird cluster", then you need to wait for each infection to progress far enough to result in hospitalization. How do the conclusions of the previous post change if we extend our model to account for a delay, but keep the goal of flagging an epidemic before 1% of people have been infected?

Recall that last time we estimated that, for something doubling weekly, when 1% of people have ever been infected then 0.69% of people became infected in the last seven days. With a delay of a week, however, by the time we learn that incidence has hit 0.69% many more people will have been infected and we'd have missed our 1% goal by a lot. The effect of delay is that during this time the epidemic will make further progress, which will depend on the growth rate: with a shorter doubling period there will be more progress. Can we get an equation relating cumulative infections to delayed incidence?

Let's call delay $d$. Instead of $\frac{i\left(t\right)}{c\left(t\right)}$ we now want $\frac{i(t-d)}{c\left(t\right)}$. That is, what's the relationship between cumulative infections and what incidence was when the information we're now getting was derived?

We can do a bit of math:

$$\frac{i(t-d)}{c\left(t\right)}=\frac{k{e}^{k(t-d)}}{e^{kt}}=k{e}^{-kd}=\frac{2\ln \left(2\right)}{T_d}{e}^{\frac{-d}{T_d}}$$

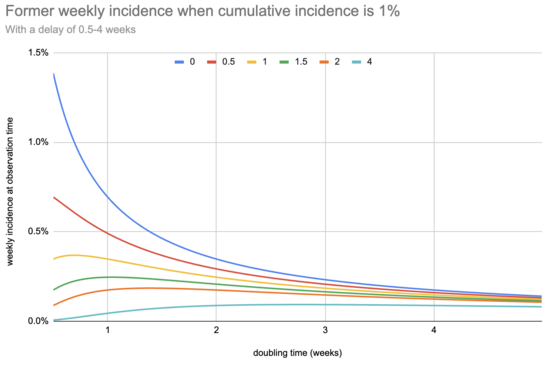
What does this look like, for a few different potential delay values?

My main takeaway is that, under these assumptions, delay matters less than I would initially have guessed: the sensitivity you need to design for is driven by the need to catch slow-growing epidemics. For example, even with up to eleven days of delay a system sensitive enough to flag an epidemic that doubles every four weeks is sensitive enough to detect one that doubles every three days.

This isn't the whole story, though, because many of the actions that you would want to do post-discovery are more urgent with higher growth rates. This means you need to count the delay of your core response (ex: implementing NPIs) in the total delay: you can't allocate the entire delay budget to the detection system.

Another thing to note is that this is all under the assumption that detection depends on incidence above a threshold, and whether this is actually the case is unclear for several potential systems. For example, with wastewater sequencing detection my current best guess is this primarily would rely on the total number of observations of the pathogen, which would be proportional to (delayed) cumulative infections and not (delayed) incidence. With detection based on cumulative infections minimizing delay matters a lot more.