On the France/Italy Power Grid expansion there are the usual six regions, but because of the way Italy is a peninsula there are fewer combinations than usual:

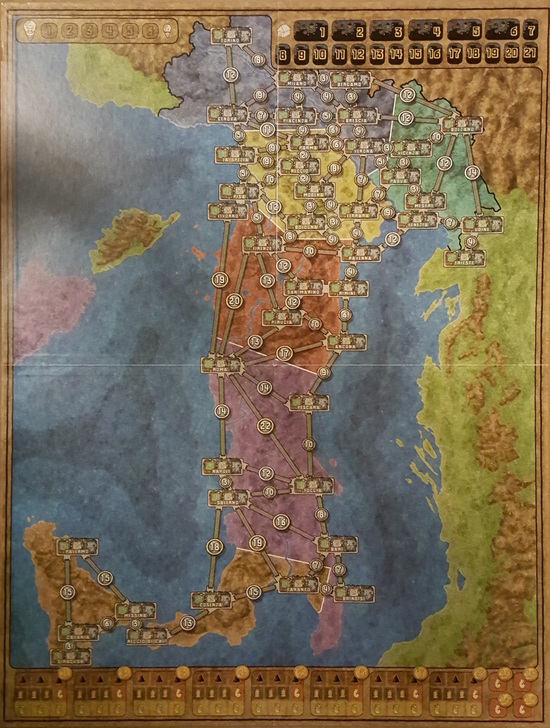
The board has six regions, Brown, Purple, Red, Yellow, Blue, and Green, and in an N player game you randomly choose N connected regions to play with. In a three player game, for example, the options are:

• Brown, Purple, Red
• Purple, Red, Yellow
• Red, Yellow, Blue
• Red, Yellow, Green
• Yellow, Blue, Green

When selecting which regions to use, though, what does "randomly" mean? Here are three ways you might consider:

• Choose three regions at random. If they're not connected, try again.

• Choose a region at random. Then from the remaining contiguous regions, choose another region at random. Repeat for the third region.

• Choose one of the five legal combinations at random.

While the first and third options give the same distribution—each of the five options 20% of the time—the second option does not:

30%	Brown, Purple, Red
17%	Purple, Red, Yellow
16%	Red, Yellow, Blue
16%	Red, Yellow, Green
21%	Yellow, Blue, Green

I think for this game "combinations" is the right thing to be selecting over, so would choose the third selection method above. But if you care more about regions than combinations, you might prefer the second method: with the even-20% method we have Yellow 80% of the time, while in the sequential method we only have it 70% of the time:

Region	Even-20%	Sequential
Brown	20%	30%
Purple	40%	47%
Red	80%	79%
Yellow	80%	70%
Blue	40%	37%
Green	40%	37%

If an even distribution over regions is our goal, however, intentionally optimizing for it can do better:

Region	Even-20%	Sequential	Region-optimized
Brown	20%	30%	50%
Purple	40%	47%	50%
Red	80%	79%	50%
Yellow	80%	70%	50%
Blue	40%	37%	50%
Green	40%	37%	50%

What does this solution look like?

50%	Brown, Purple, Red
0%	Purple, Red, Yellow
0%	Red, Yellow, Blue
0%	Red, Yellow, Green
50%	Yellow, Blue, Green

Which shows, I think, that uniformly selecting over combinations of regions is what we want.